Modeling Soft Robots
Comparing Different Models
There is no golden rule for modeling soft robots and often the solution relies on data availability, physical propertiese, and the computation time at disposal.
When describing a soft robots, we always balance accuracy and computational cost.
Nevertheless, having a control-oriented and accurate model increases performances of the planning and control phases.

Euler-Bernoulli Beam

Cosserat Rod Theory

Piecewise Constant Curbature

Lumped Parameter (WINNER 🎉🎉)

Real Robot
These videos displays the different behaviors of a fishing rod robot when using different models and subjected to the same input torque \( u(t) = \cos(4 \pi t) \).
Relative Degrees May Change \(\rightarrow\) Be Aware!
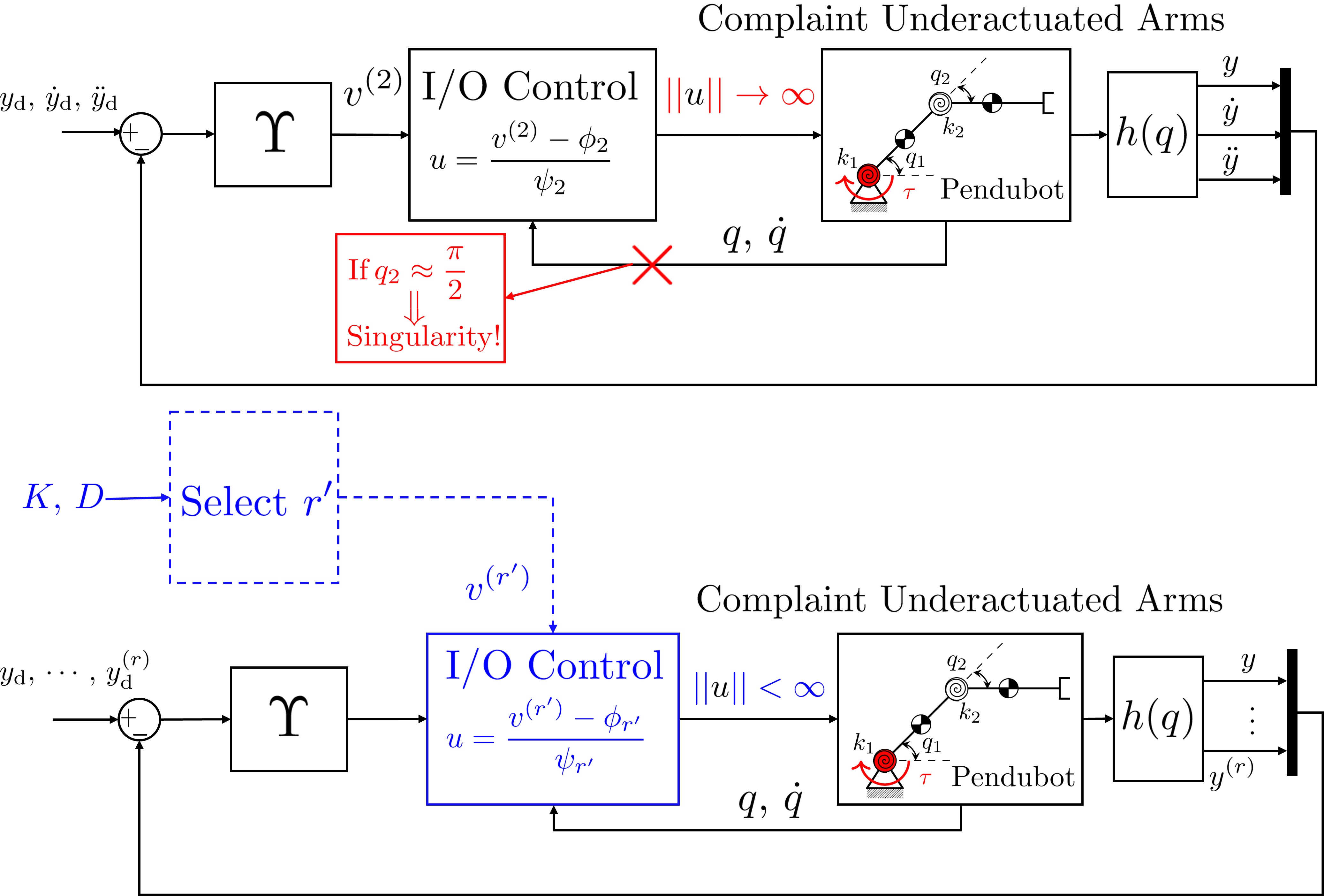
Due to underactuation, the relative degree of complaint underactuated robots may change leading to singularities in model-based control.
We study high-order controllability conditions to ensure a constant relative degree and, interstling enough, this can be guaranteed by the presence of the elastic elements.
We investigate this property in the following paper Dynamic Coupling for Underactuated Compliant Arms With Not Well-Defined Relative Degree (IEEE TSMC:S)
The main idea is to use high-order controllability conditions to be used in the control action.
In the classic case, \( u(t) = \dfrac{v^{(2)} - L_f^2h(x)}{L_gL_fh(q_1,x)} \to \infty \) if \( q_1 \to 0 \) where \(h(\cdot)\) is the output function.
Proposed solution for any underactuated robots: \( u(t) = \dfrac{v^{(r')} - L_f^{r'}h(x)}{\varphi_{r'}(x, K, D)} < \infty, \, \forall x \in \mathbb{R}^{2n} \)
Below, we show the behavior of a 3PCC robot with different relative degrees \( r' \) and the presence of singularities.

3PCC with \( r'=2\) singularity in \(t=2.44\)sec
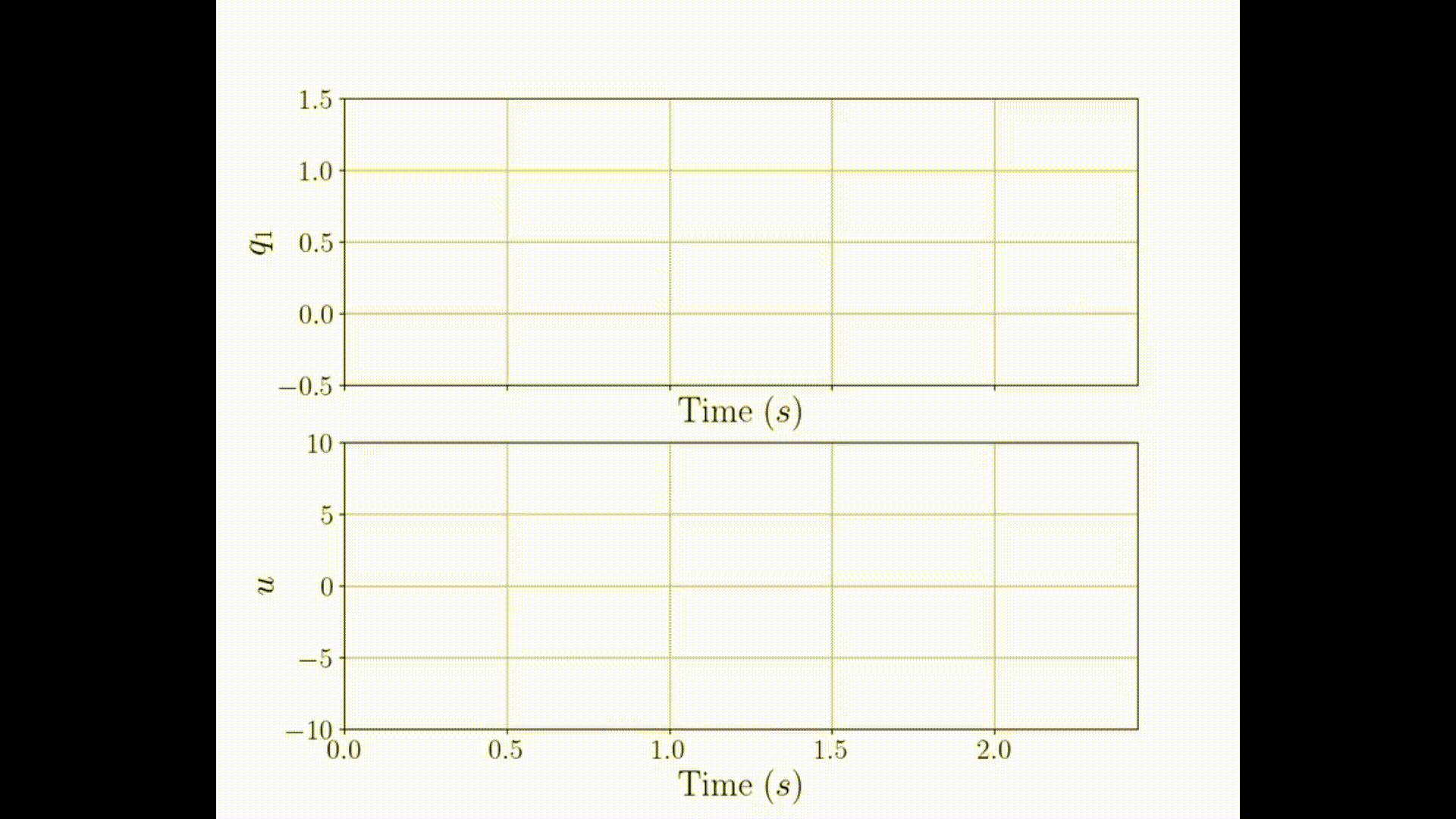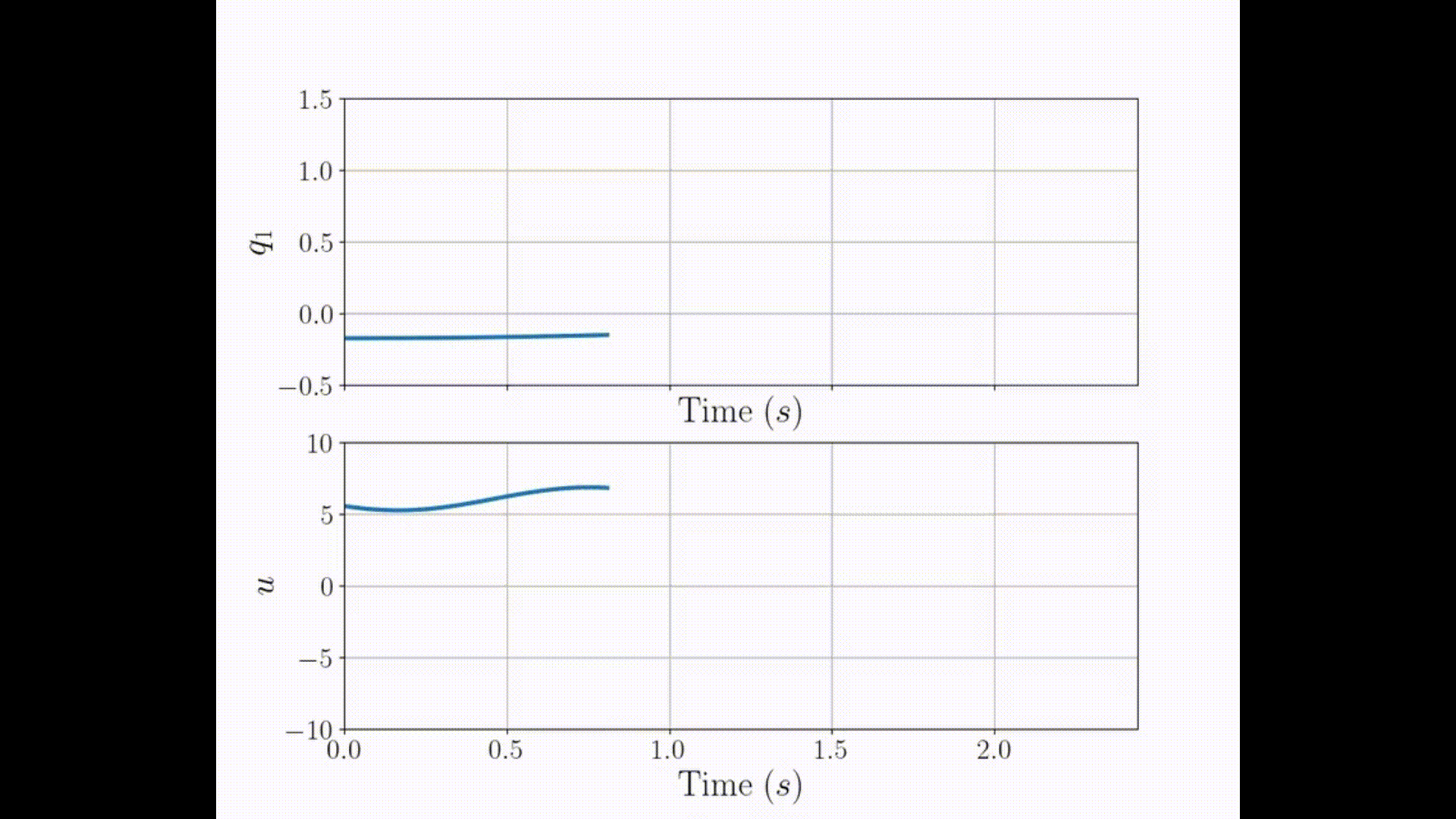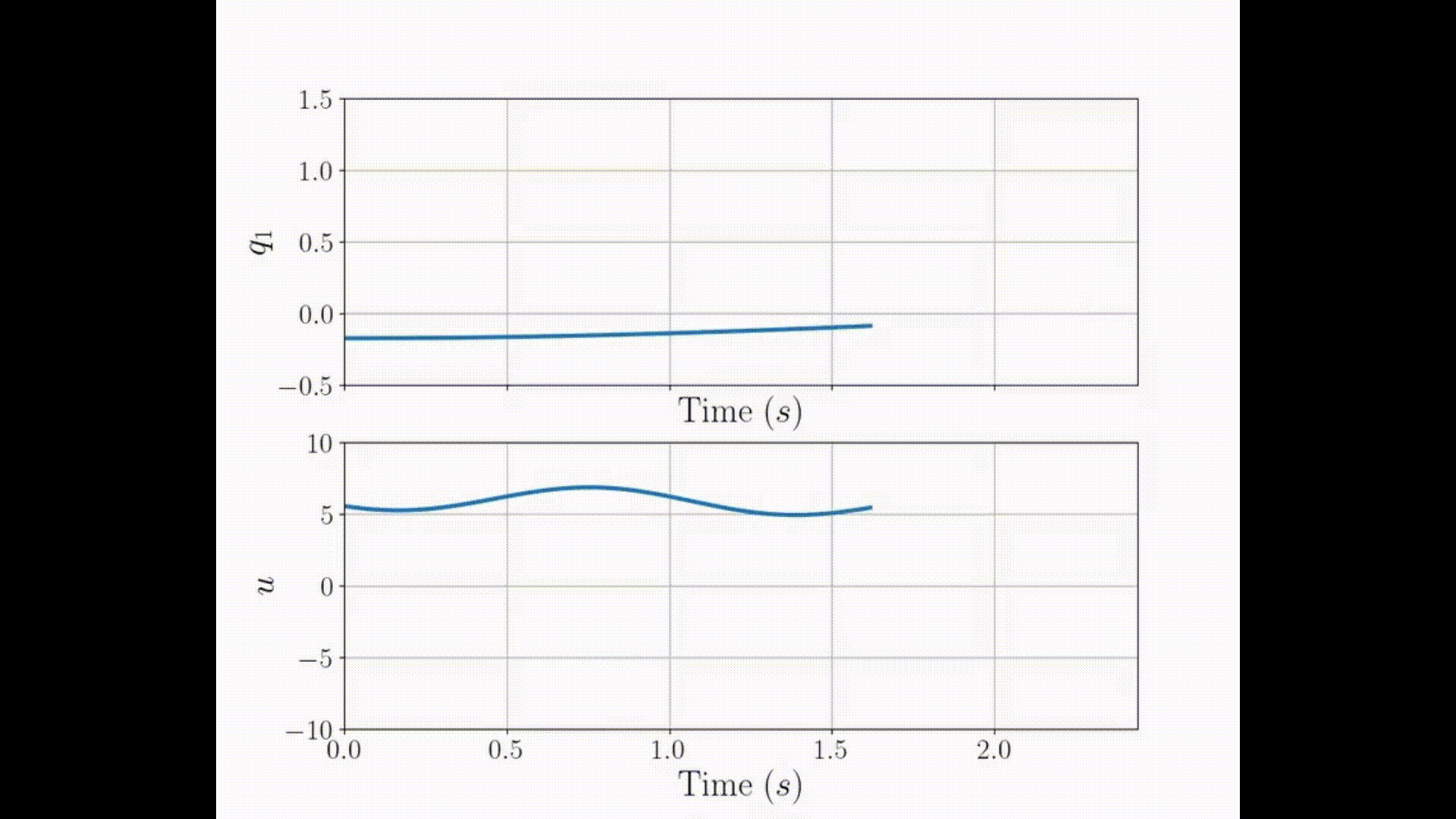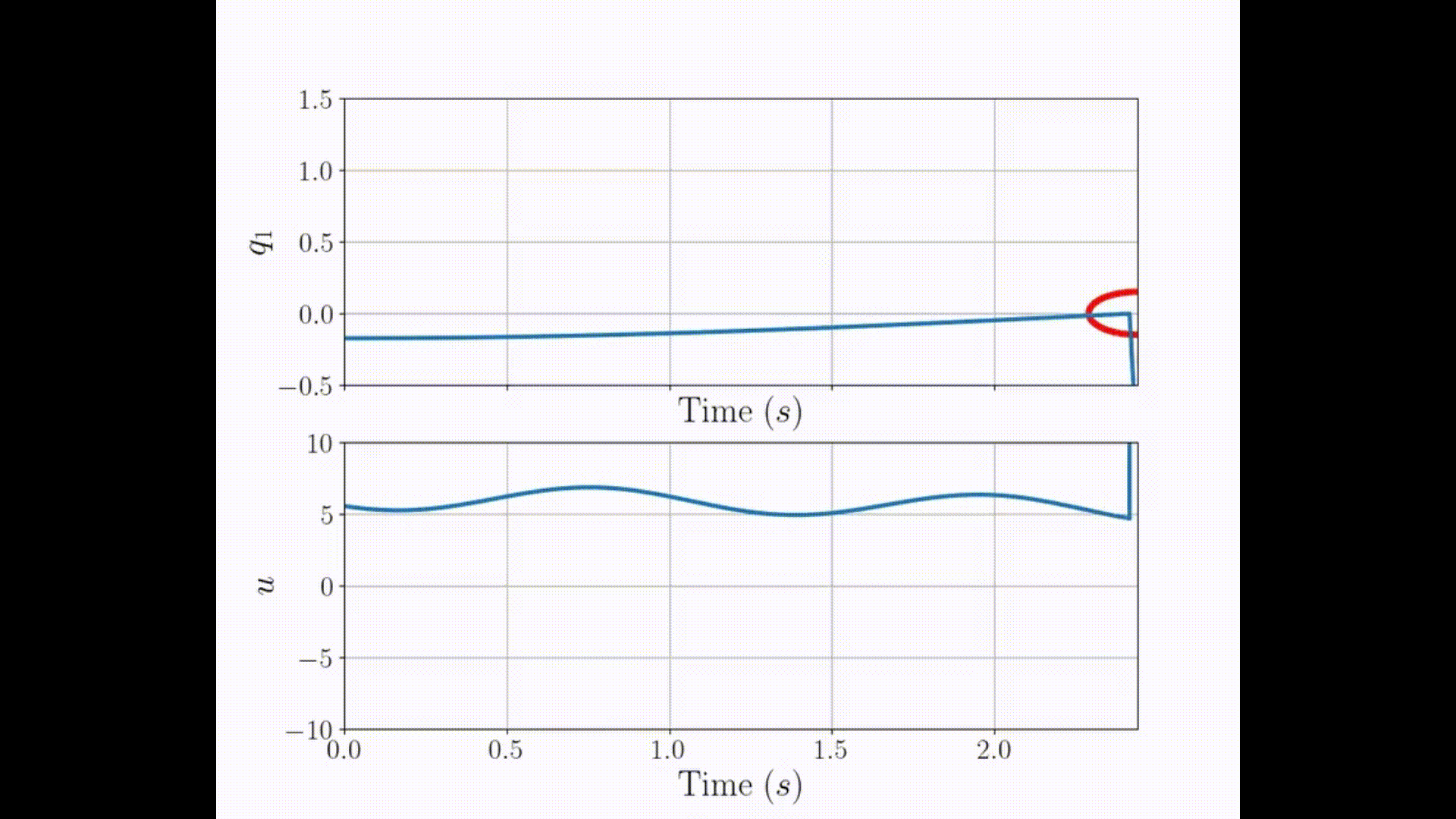
3PCC with \( r'=2\) singularity in \(t=2.44\)sec

3PCC with \( r'=3\) NO singularity
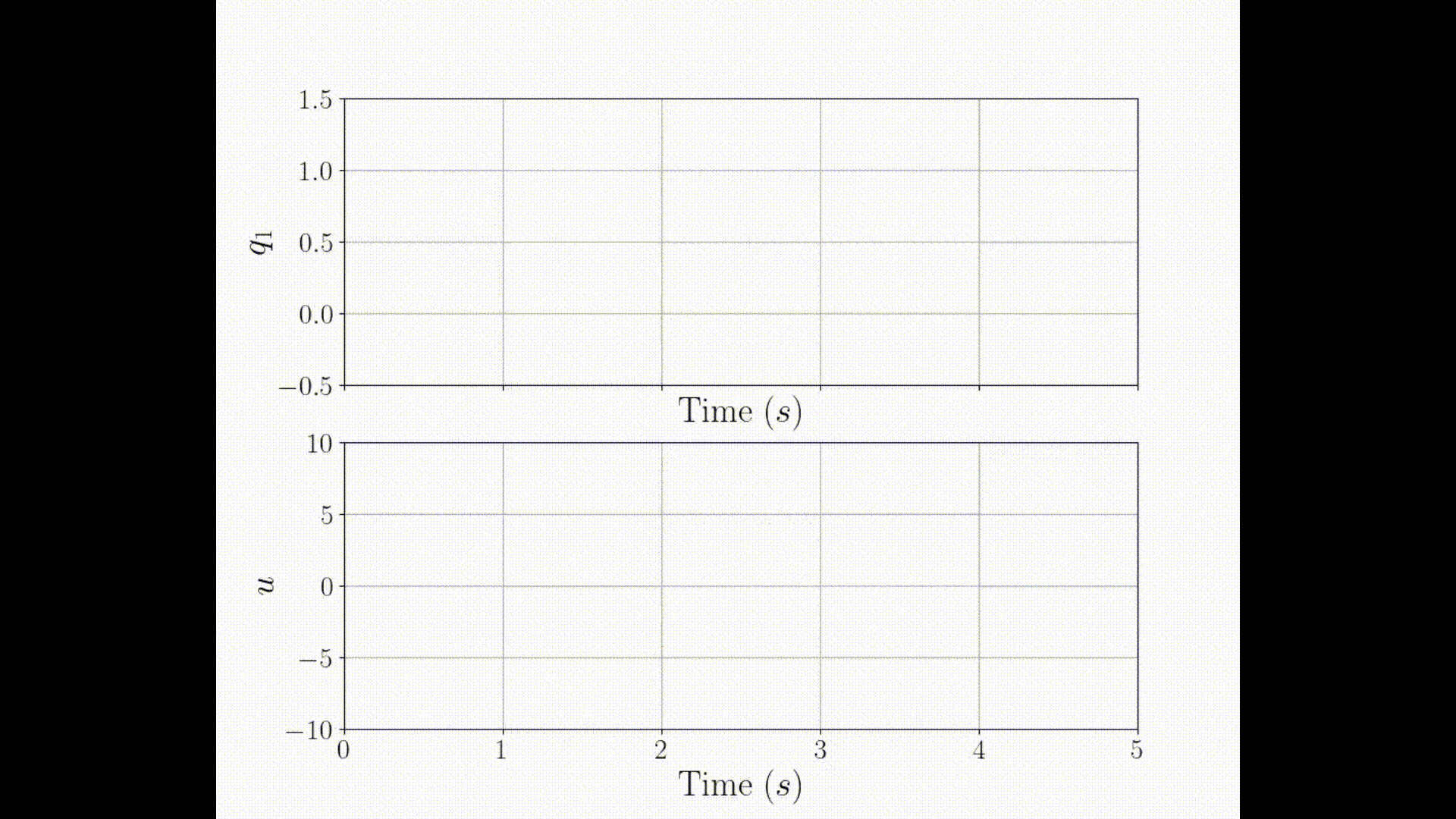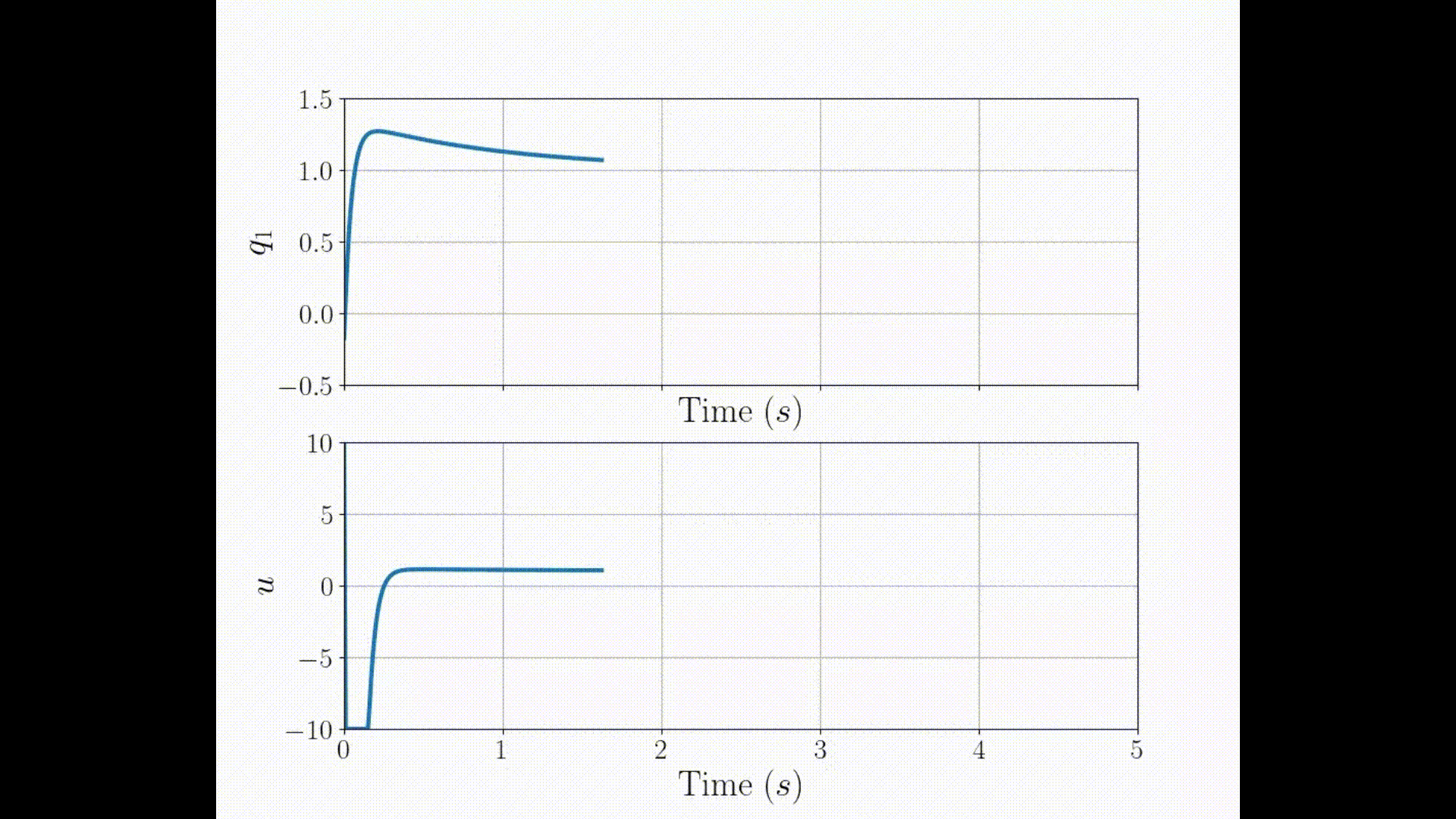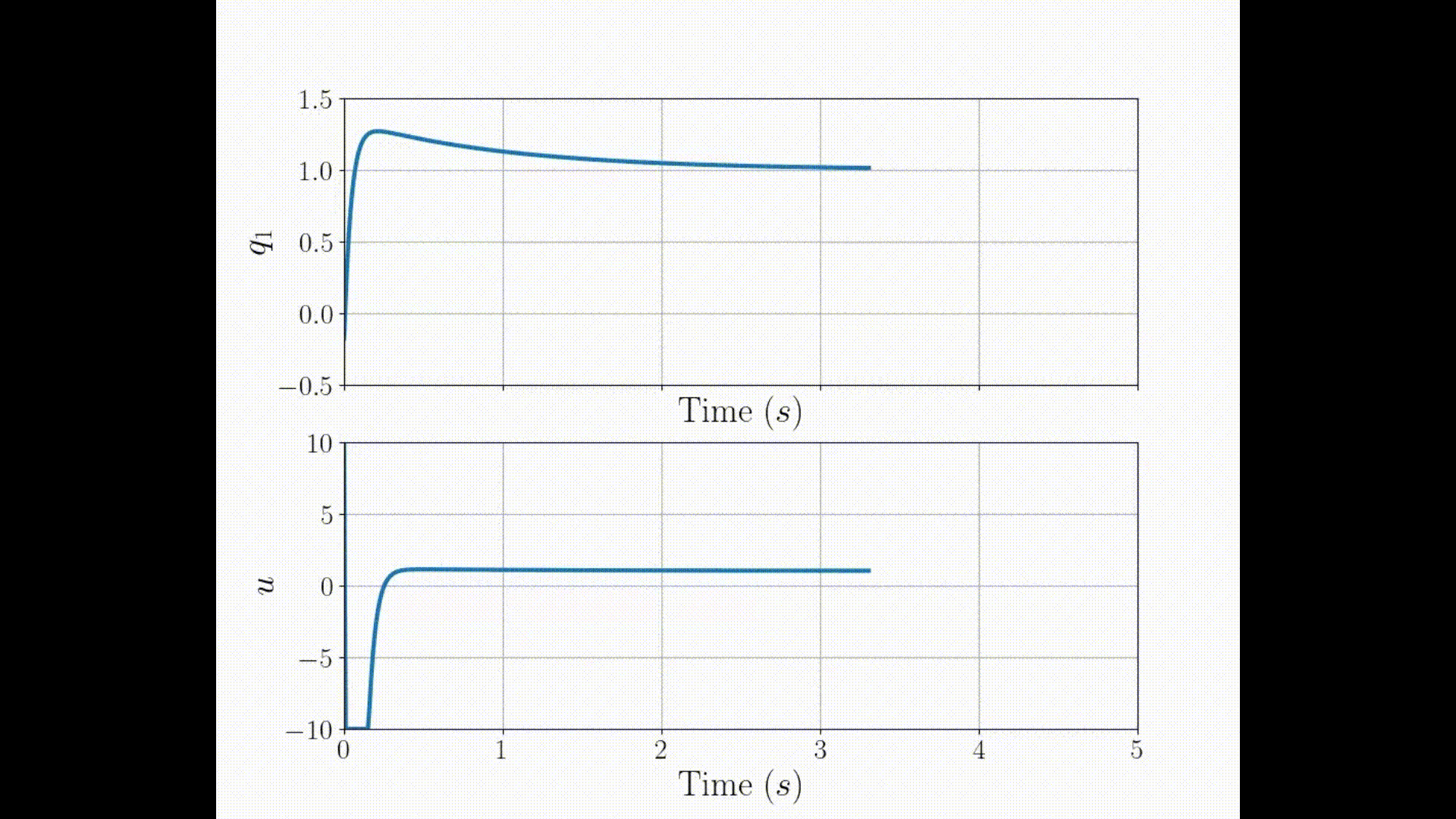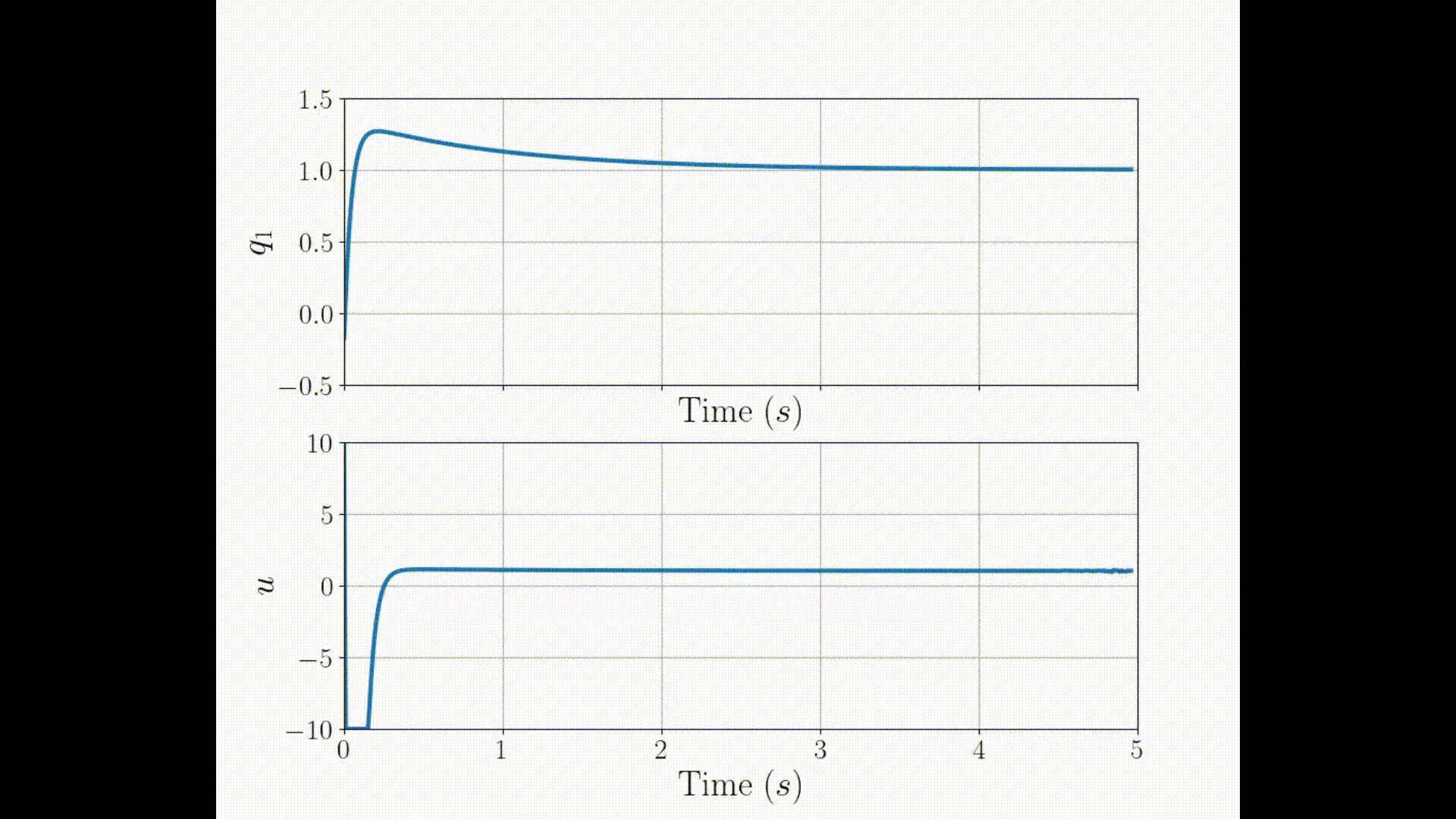
3PCC with \( r'=3\) NO singularity
Design of Multimodal Robots




In the design of multimodal robots, we are exploiting mixed features to combine locomotion and vehicle behavior.

